
Le livret complet relatif à l’événement de cette année scolaire est téléchargeable à l’adresse : https://syncandshare.desy.de/index.php/s/f8PfxsW3kHCaCz4
Pour la journée internationale cosmique 2024 ou ICD 2024, un groupe d’une dizaine d’élèves de Sciences + ont réalisé des mesures à l’aide de deux détecteurs : La “Roue Cosmique” du dispositif “Sciences à l’Ecole” conçue au CCPM de Marseille et la mallette “Cosmix” du CENBG de Bordeaux.


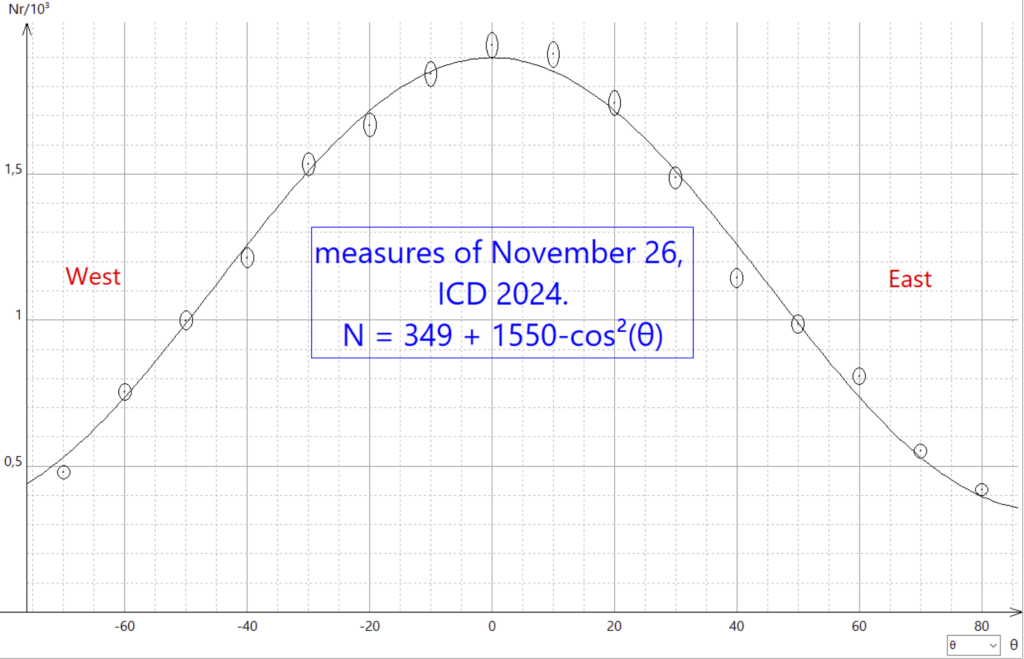
Les documents suivants présentent les résultats obtenus pour une orientation Est-Ouest de la « Roue ». L’incertitude sur l’angle azimutal est de ±1° . L’incertitude sur le nombre N de muons est √N. La modélisation par une fonction en cos2 θ est très satisfaisante.
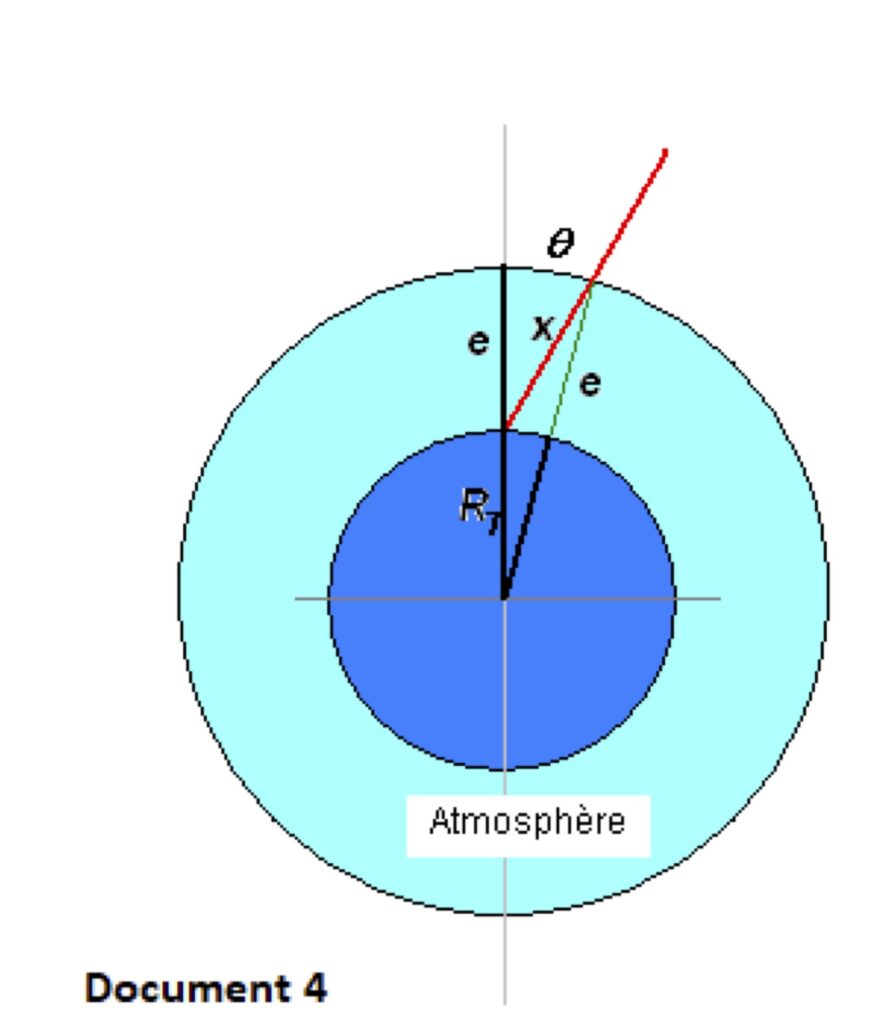
Nous avons calculé la distance additionnelle parcourue par un muon arrivant sous un angle non nul (doc. 4)
La figure montre que
(RT+e)2 = RT2 + x2 – 2x.RT.cos(π-θ)
ce qui mène à la résolution de l’équation :
RT2 + x2 – 2x.RT.cos(π-θ) – (RT+e)2 = 0
La solution positive est
x= √( RT2cos2θ+e2+ 2eRT) – RT.cosθ
Comme exemple, on peut prendre un muon qui arrive sous une inclinaison de 30°. Nous obtenons alors x = 35 km pour une épaisseur de l’atmosphère de 30 km (nous supposons que ce muon est produit à 30 km d’altitude). Ainsi, en tournant la roue de 30°, on ajoute une couche d’atmosphère d’une épaisseur de 5 km !
Nous avons examiné les paramètres qui changeraient le nombre de muons de 1941 ±44 (à θ=0) à 1488±39 (à θ=30°).
– La désintégration des muons sur les 5km.
– L’énergie perdue en traversant l’air
– La dilatation des durées.
Les élèves ont perçu la difficulté du problème pour différentes raisons et en particulier à cause du fait que les muons n’arrivent pas à la même vitesse ! On montre que les probabilités de désintégrations en cours de route varient entre 10% et 30% …
En tenant compte de ce qui précède, le nombre de muons devrait varier de 1941 à 0.7×1941≤ N≤0.9× 1941,soit 1359 ≤ N≤1750.
Nous avons trouvé à 30° N = 1488 après un parcours supplémentaire de 5 km, ce qui est satisfaisant comme résultat.



